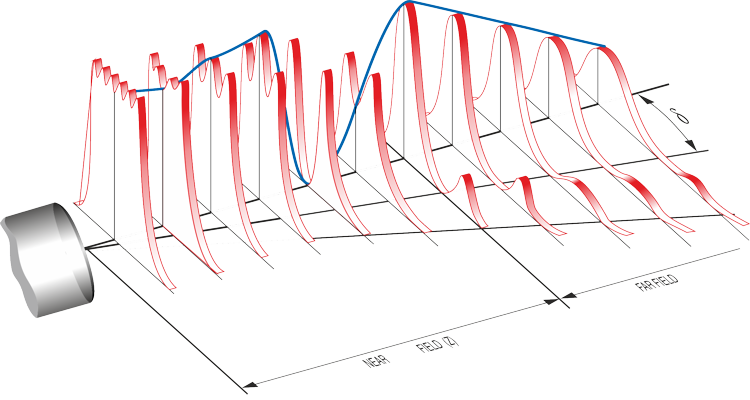
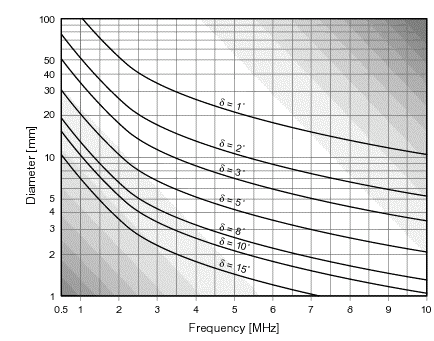
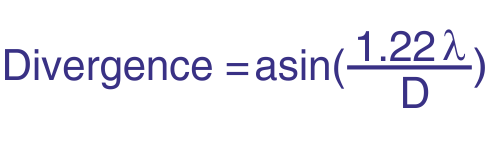In Doppler echography, the goal is not to use a plain longitudinal wave, but rather an ultrasonic beam that is as thin as possible throughout the measurement depth. The geometry of the acoustic field is governed by the diameter D of the emitter and the wavelength λ of the ultrasonic waves, which is equal to the ratio of the sound velocity in the analyzed medium to the emitting frequency. The typical shape of the ultrasonic field is illustrated in the figures below, which show two particular zones.