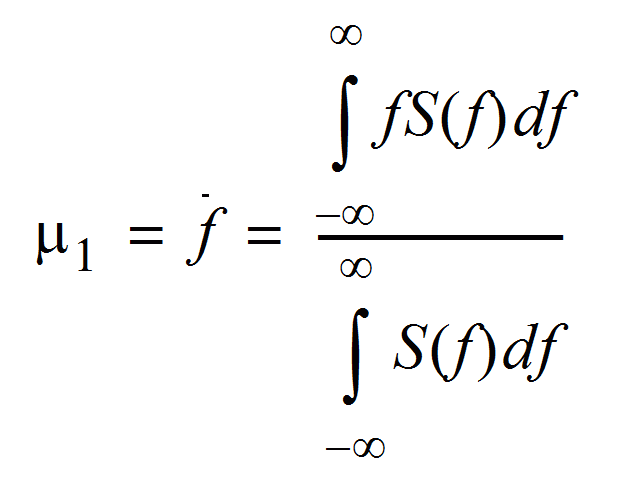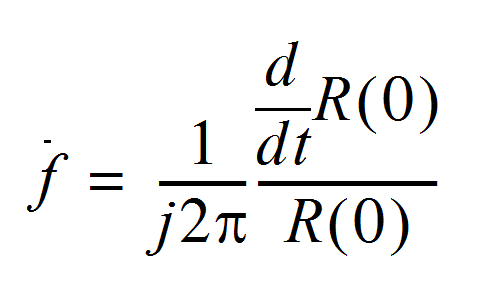The amplitudes of the echoes reflected by the particles within the flowing fluid are somewhat
random in nature, corresponding to the random distribution of the particles in the fluid medium.
Thus, the Doppler signals may be treated as random processes, and characterized by different moments.
In order to be able to determine the probability of occurrence of this process, one must have
access to a great number of actual occurrences of the process. In practice, it is difficult
to obtain measurements of the exact same process under the exact same conditions at several
different times. Therefore, a temporal average is preferable to an ensemble average.
The temporal average and the ensemble average will not be the same unless the process is
stationary and the analysis time is very long (tending to infinity). Considering the
Doppler process as stationary, the average frequency may be expressed as the normalized first moment,
where S(f) is the spectral density or probability density of the Doppler signal.