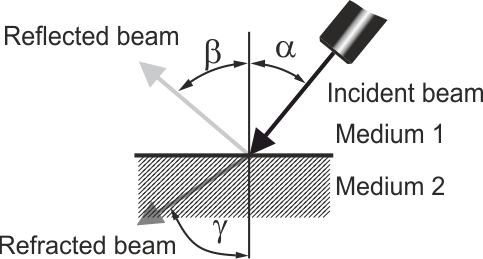
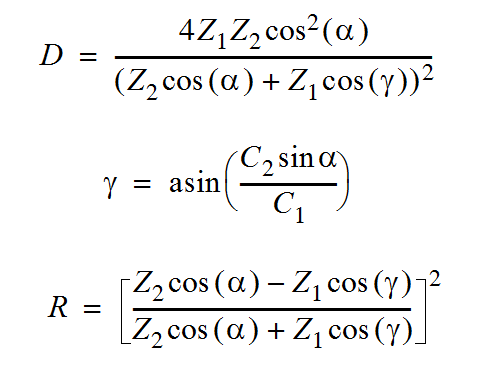The simple equations below assume a plane infinite wall or interface.
This is of course never the case. Nevertheless, these three equations
could really help because:
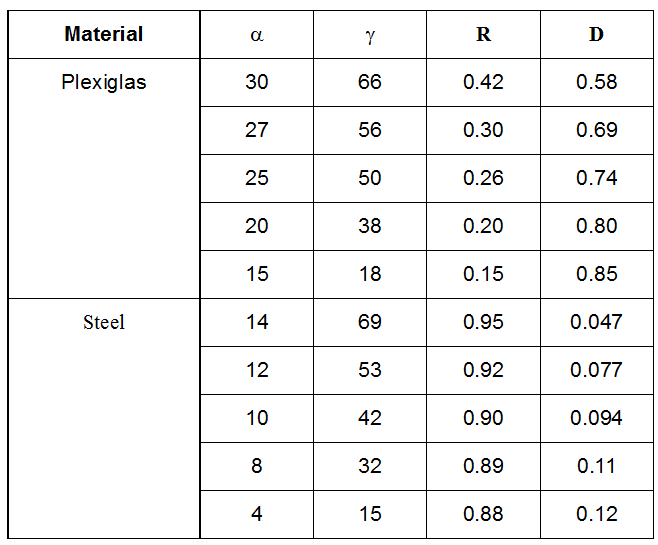
- they give an approximation of the total reflection angle.
- they predict the amount of ultrasonic energy that will penetrate in the liquid.
- they predict the amount of energy that tends to remain in the wall.
where:
Zi is the acoustic impedance of the medium i, which is equal to the
product of the sound speed by the density of the medium i;
R is the ratio of the reflected intensity to the incident intensity;
D is the ratio of the refracted intensity to the incident intensity.